洋上風力エネルギー分野の研究

1. 洋上風力発電
 2. 海洋エネルギー利用施設の浮体式支持基盤の波浪中弾性応答解析法の開発

1. 洋上風力発電

風力発電はポテンシャルが大きく、特に洋上は風が強く乱れが少ない、設置可能場所が広大等の利点がある。欧州では大規模な洋上ウィンドファームが稼動しているが、全て海底に基礎を置く着床式である。着床式は、水深50mまでが限界なため、さらなる展開に向けて様々な浮体式が研究されている。これらの内、スパー型は実用化に最も近いもののひとつである。海洋エネルギー研究所では、低コスト化を図れる簡易な構造で波浪中動揺の少ない新しいスパー型の研究を行っている。


従来型スパー（Hywind）*1	トラス・スパー（Technip）*2

出典

*1　Statoil社Webサイト　　　　
*2 Technip社Webサイト

従来の風力発電用スパーは単純な円筒構造である。一方、石油・ガス開発の分野ではトラス・スパーが既に実用化しており、ヒーブ・プレートと呼ばれる水平板で上下の動揺を抑えている。しかし、風力発電では傾斜を抑えることが重要なため、鉛直方向に減揺プレートを入れる構造を考案し、水槽実験によって運動を比較した。


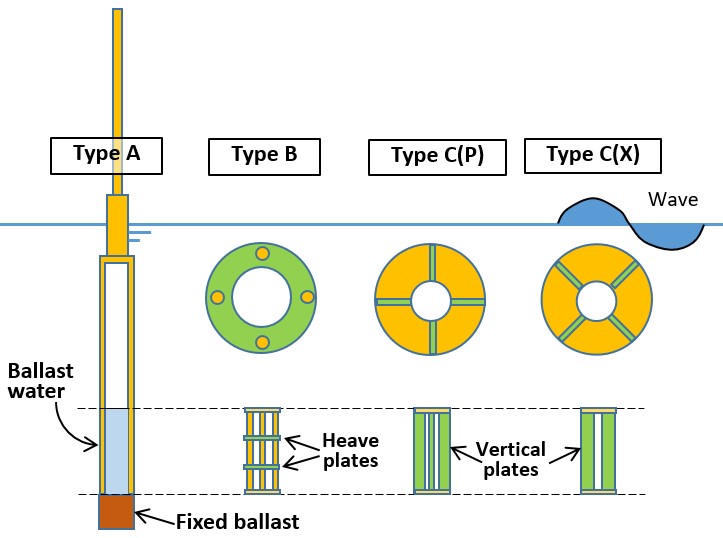水槽実験模型	交換部（左からB型、C型、A型）

規則波中実験によって周波数応答関数（RAO）を比較した結果、ナセル部（タワー頂部）の水平加速度が、従来型に比べほぼ全周波数で減少する等、C型の動揺低減が確認された。この構造は高い水圧が作用する部分を非水密の平板構造としており、コスト面でも利点があると考えられる。減揺プレートの最適化により、さらに改良を行う予定である。


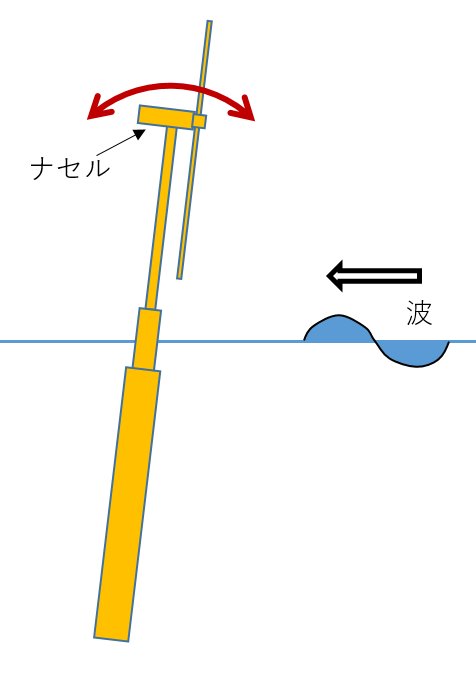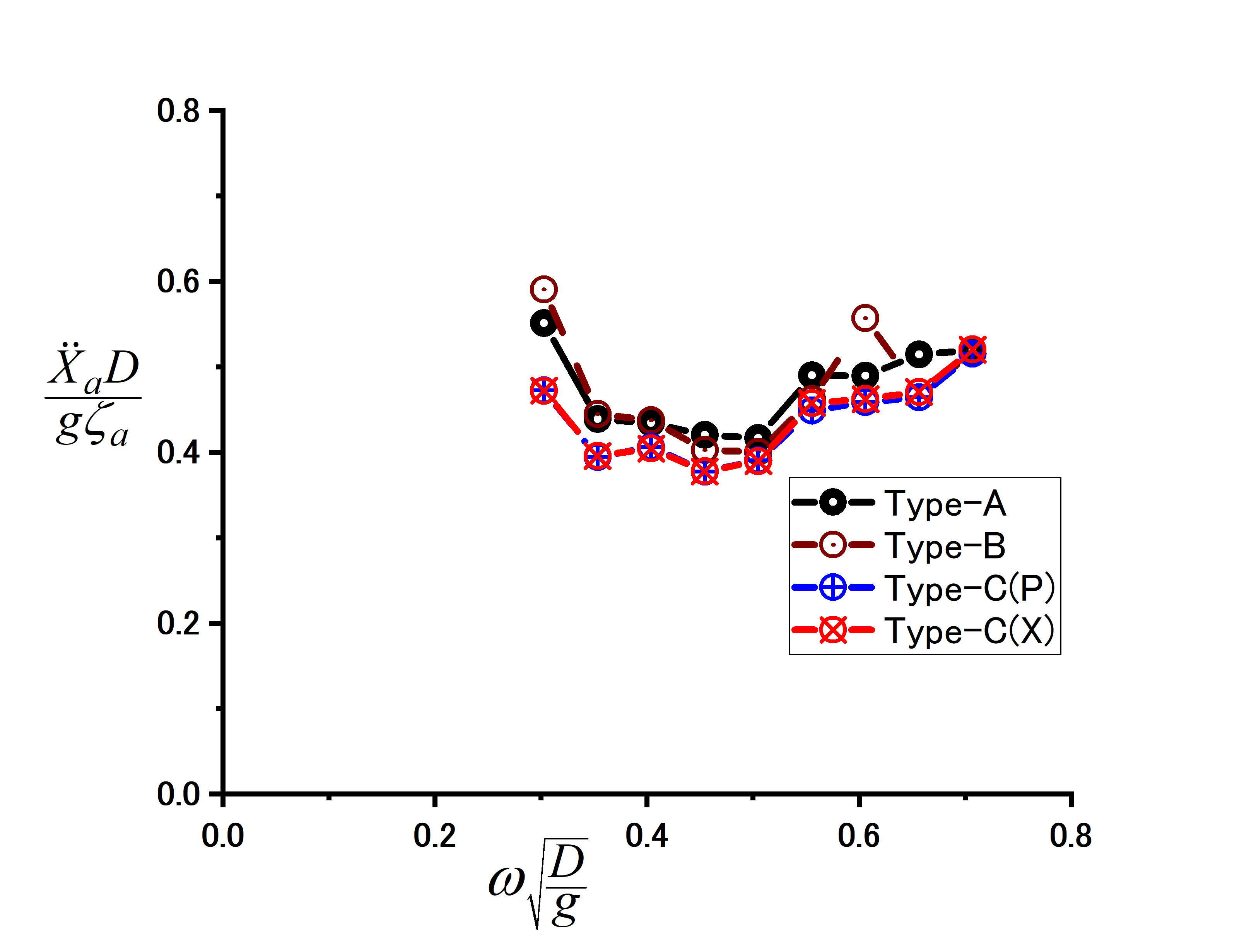	ナセル水平加速度の周波数応答関数

2. 海洋エネルギー利用施設の浮体式支持基盤の波浪中弾性応答解析法の開発

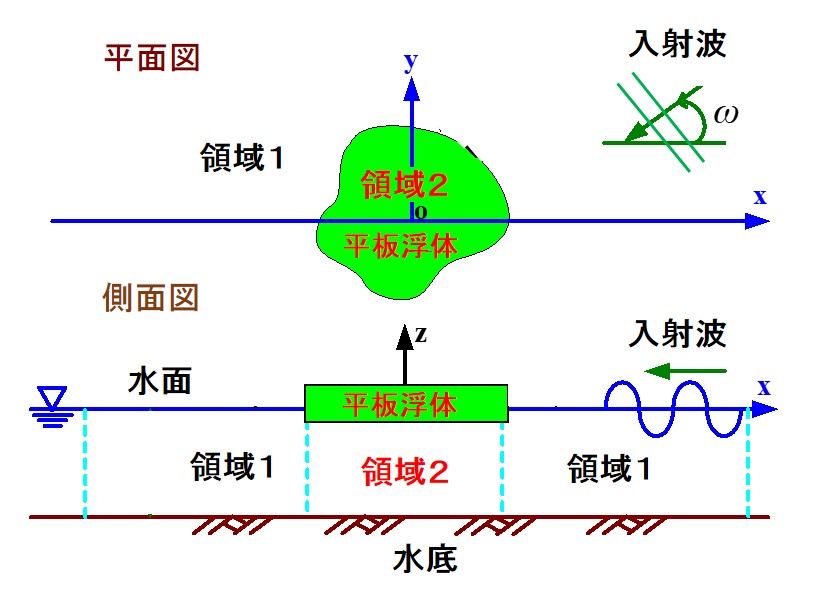
　多数の風力発電装置や海洋温度差発電等の海洋エネルギー利用施設を洋上に設置するための支持基盤として様々な形式の浮体構造物が提案されています。それらの中で平板型浮体構造物は最も基本的な構造で、現在、平面的にロの字の浮体形状を持つ浮体式風力発電装置も建設中です。このような平板構造浮体では、浮体構造の大型化に伴い、波浪中で上下方向に弾性変形が現れるので、構造設計においてはこの弾性応答を考慮することが必要です。

図１海域に設置された複雑な平面形状を持つ平板浮体

このような目的から、研究所では、多数の風力発電施設搭載用の平板浮体の初期設計に適した波浪中弾性応答解析法を開発しました。提案した方法は、以下のような特徴を持っています。

①   流体の解析には非圧縮非粘性流体の渦無し流れを考え、速度ポテンシャルを仮定して、浮体には平板理論を用いる。
②   構造と流体の連成問題を対象として、浮体の喫水は零として扱い、浮体の存在（平板浮体の上下方向の運動方程式等）は、流体問題の境界条件として扱う。
③   水面下部（図１、領域１）と浮体下部（領域２）の２つの流体領域のそれぞれに関して、固有関数展開法を適用する。領域２の流体に関する固有関数展開を、研究所で新しく示した構造と流体の運動を規定する４種類の変分原理の内の、流体運動に関係する速度ポテンシャルのみで表現した変分原理に代入して、最終的に、領域２の固有関数展開の未知関数を含んだ、浮体端部に関する境界積分方程式を導く。
④   ③で得られた浮体端部に関する境界積分方程式と、流体の領域１の固有関数展開に含まれる未知関数に関する境界積分方程式を連立させて解くことにより、２つの流体領域の固有関数展開に関する全ての未知関数を求めることができる。最終的に、２次元的な水面波が、平板浮体に入射した時の浮体の上下変位分布と浮体周辺の水面変位分布を求めることができる。

この計算法は、平面的に様々な形状の平板浮体に適用可能で、超大型の浮体式浮体空港等の計算にも適用できます。

図２　水面に浮かんだ平板浮体

図３　矩形平板の上下方向変位振幅の分布
（ w：上下方向変位振幅、 ζ₀：入射波振幅）

図３は、図２に示した長さ1200m、幅240mの矩形平板浮体に、周期8.4secの規則波が、浮体の長手方向（ ω= 0度）に入射した時の浮体の上下方向変位振幅分布を示したものです。 wは浮体の上下方向変位振幅、 ζ₀は入射波振幅です。
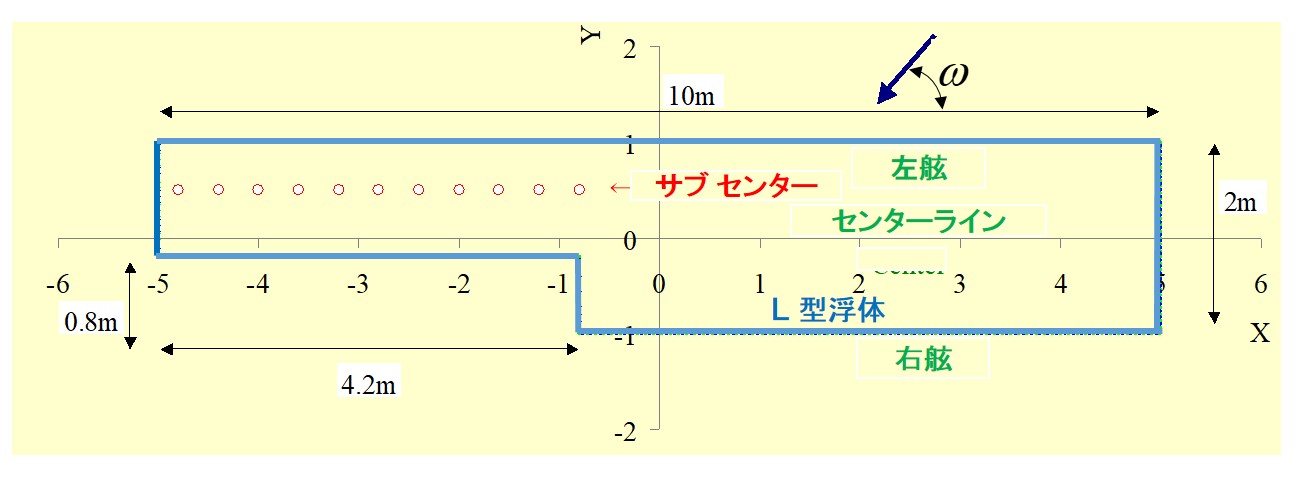
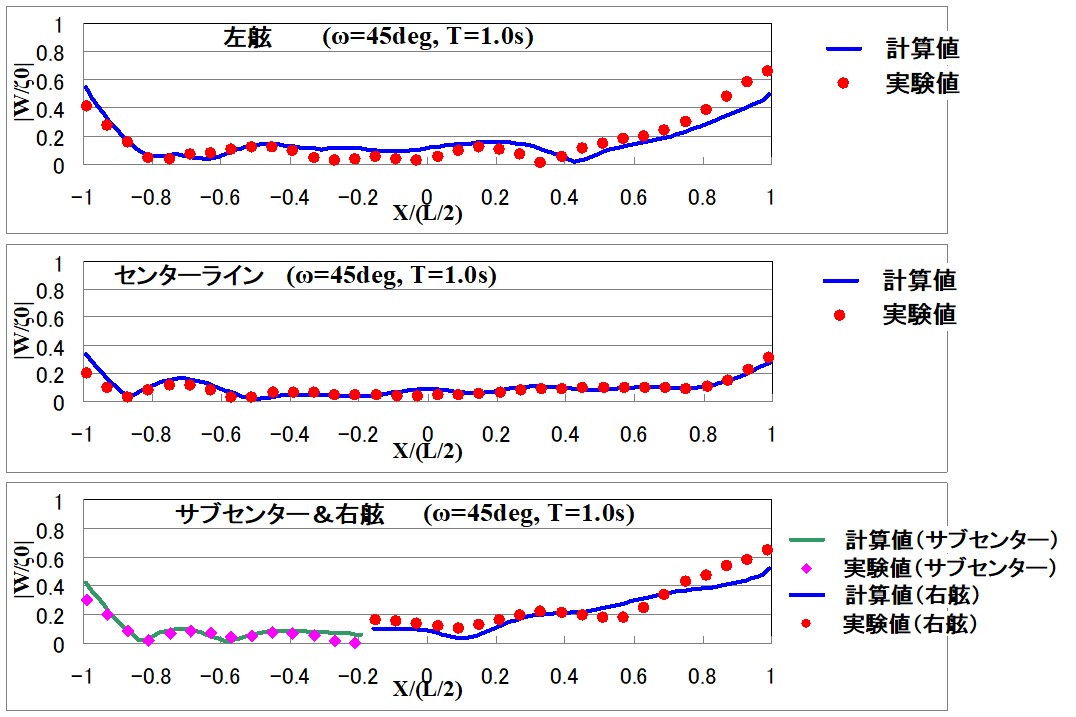
図５は、図４に示した長さ12m、幅2mのL型の平面形状を持つ平板浮体の実験モデルに、 ω=45度の角度で周期T=1秒の規則波が入射した時の、左舷、センターライン、サブセンター＆右舷位置における、浮体の上下方向変位振幅の浮体長手方向分布に関する計算値と実験値を比較したものです。計算値と実験値は良く一致しており、計算法の有効性が示されました。

図４　L型平面形状を持つ平板浮体

図５　浮体の長手方向の上下方向変位振幅の分布
　　（左舷、センターライン、サブセンター＆右舷の位置）